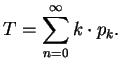Taking A random walk in a city -- but will I get back home?
Marek R. Rychlik
Imagine that you are stranded in an infinite city, in which streets
and avenues run from the south to the north, and from the west to the east, and
are separated by a distance of one mile. Let us assume that
the streets and avenues are numbered by integers, both positive and negative,
and that you live at the intersetion of 0th Avenue and 0th Street.
Suppose that you want to take walk in the city. That is a random walk.
Every time you are at the intersection you are going to toss a coin twice,
to determine which of the four possible directions to take.
Assume that you walk 1 mile a minute.
Here are the questions?
- What is the probability that you will be home in not more than 10 minutes?
- How long on the average will it take you to get back home,
i.e. to the intersection of 0th Avenue with 0th Street?
Let your current position be 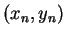 where
where 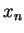 and
and 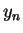 are the
number of the avenue and the street that you are on after
are the
number of the avenue and the street that you are on after 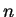 minutes
of walking. Now you need to draw two numbers,
minutes
of walking. Now you need to draw two numbers, 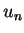 and
and 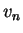 from the
set
from the
set 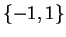 with replacement (i.e. after you have drawn a number,
you immediately put it back in the set). Obriously, the situation
in the problem can be modelled by the following system of difference equations:
with replacement (i.e. after you have drawn a number,
you immediately put it back in the set). Obriously, the situation
in the problem can be modelled by the following system of difference equations:
Now, suppose that you have created a random sequence of 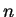 pairs
pairs
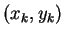 ,
,
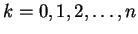 . If for some
. If for some 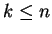 both
both 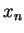 and
and 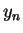 are zero then obviously you returned home in
are zero then obviously you returned home in 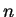 minutes.
Compute the probability of returning home in exactly
minutes.
Compute the probability of returning home in exactly 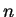 minutes as
follows.
minutes as
follows.
First, fix two numbers 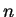 (the length of sequence) and
(the length of sequence) and 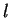 (the
number of runs). In each run, classify the sequences by the minimal
value of
(the
number of runs). In each run, classify the sequences by the minimal
value of 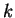 for which
for which 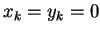 .
Let
.
Let 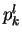 be the number of such sequences divided by
be the number of such sequences divided by 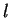 . Ideally,
you would define the probability of returning in
. Ideally,
you would define the probability of returning in 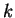 minutes as:
minutes as:
The average time of returning home is:
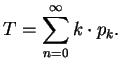 |
(1) |
Taking A random walk in a city -- but will I get back home?
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 randomwalk.tex
The translation was initiated by Marek Rychlik on 2003-09-26



Marek Rychlik
2003-09-26
![]() (the length of sequence) and
(the length of sequence) and ![]() (the
number of runs). In each run, classify the sequences by the minimal
value of
(the
number of runs). In each run, classify the sequences by the minimal
value of ![]() for which
for which ![]() .
Let
.
Let ![]() be the number of such sequences divided by
be the number of such sequences divided by ![]() . Ideally,
you would define the probability of returning in
. Ideally,
you would define the probability of returning in ![]() minutes as:
minutes as: